Rozkład t-studenta – teoria
Rozkład t-studenta(nazywany również rozkładem t lub po prostu rozkładem studenta) jest rozkładem prawdopodobieństwa wykorzystywanym do testowania hipotez statystycznych, oceny błedów pomiaru oraz konstruowania przedziałów ufności. Do wyznaczenia jego wartości używana jest tablica rozkładu t-studenta
Kiedy używamy rozkładu t-studenta?
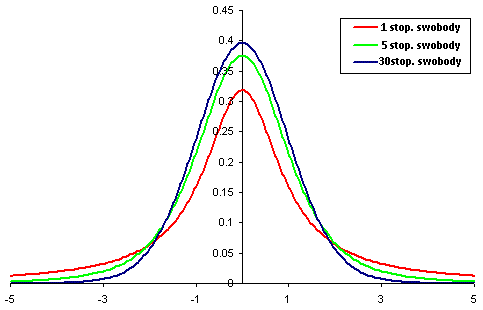
Rozkład t-studenta stosowany jest wyłącznie w sytuacjach kiedy nie jest znane odchylenie standardowe, a liczba obserwacji(rozmiar próby) jest mniejsza od 30. Jeżeli liczba obserwacji jest większa lub równa 30, zamiast rozkładu t-studenta wykorzystujemy rozkład normalny. Spowodowane jest to tym, że dla n>30 rozkład studenta jest bardzo zbliżony do rozkładu normalnego. Dla n<30 rozkład t-studenta jest bardziej “rozciągnięty”, co oznacza że bardziej prawdopodobne są wartości silnie odbiegające od średniej, niż w przypadku rozkładu normalnego.
Własności rozkładu t-studenta:
- Rozkład t-studenta używany jest w sytuacjach gdy nie jest znane odchylenie standardowe populacji
- Dla n>=30 zamiast rozkładu t-studenta korzystamy z rozkładu normalnego N(0,1)
- Dla n-obserwacji rozkład t-studenta ma n-1 stopni swobody
- Jest symetryczny
- Jest jednokładny
Odchylenie standardowe – częsty błąd:
Często w zadaniach podane jest odchylenie standardowe, nie oznacza to jednak że jest to odchylenie standardowe populacji.
Np. Jeśli w treści zadania znajduje się informacja, że rozkład wielkości butelek w pewnym sklepie jest zmienną o odchyleniu standardowym 4 to jest to równoważne z tym, że odchylenie standardowe populacji wynosi 4. Jednak w przypadku gdy dana jest informacja, że wzięto 200 butelek i na ich podstawie wyznaczono odchylenie standardowe równe 3.4, oznacza to że odchylenie dotyczy tylko tej grupy, a odchylenie standardowe populacji jest nieznane.
| k\p | 0,5 | 0,2 | 0,1 | 0,05 | 0,02 | 0,01 | 0,005 | 0,002 | 0,001 |
| 1 | 1,0000 | 3,0777 | 6,3138 | 12,7062 | 31,8205 | 63,6567 | 127,3213 | 318,3088 | 636,6192 |
| 2 | 0,8165 | 1,8856 | 2,9200 | 4,3029 | 6,9646 | 9,9248 | 14,0890 | 22,3271 | 31,5991 |
| 3 | 0,7649 | 1,6377 | 2,3534 | 3,1824 | 4,5407 | 5,8409 | 7,4533 | 10,2145 | 12,9240 |
| 4 | 0,7407 | 1,5332 | 2,1318 | 2,7764 | 3,7469 | 4,6041 | 5,5976 | 7,1732 | 8,6103 |
| 5 | 0,7267 | 1,4759 | 2,0150 | 2,5706 | 3,36490 | 4,0321 | 4,7733 | 5,8934 | 6,8688 |
| 6 | 0,7176 | 1,4398 | 1,9432 | 2,4469 | 3,1427 | 3,7074 | 4,3168 | 5,2076 | 5,9688 |
| 7 | 0,7111 | 1,419 | 1,8946 | 2,3646 | 2,9980 | 3,4995 | 4,0293 | 4,7853 | 5,4079 |
| 8 | 0,7064 | 1,3968 | 1,8595 | 2,3060 | 2,8965 | 3,3554 | 3,8325 | 4,5008 | 5,0413 |
| 9 | 0,7027 | 1,3830 | 1,8331 | 2,2622 | 2,8214 | 3,2498 | 3,6897 | 4,2968 | 4,7809 |
| 10 | 0,6998 | 1,3722 | 1,8125 | 2,2281 | 2,7638 | 3,1693 | 3,5814 | 4,1437 | 4,5869 |
| 11 | 0,6974 | 1,3634 | 1,7959 | 2,2010 | 2,7181 | 3,1058 | 3,4966 | 4,0347 | 4,4370 |
| 12 | 0,6955 | 1,3562 | 1,7823 | 2,1788 | 2,6810 | 3,0545 | 3,4284 | 3,9296 | 4,3178 |
| 13 | 0,6938 | 1,3502 | 1,7709 | 2,1604 | 2,6503 | 3,0123 | 3,3725 | 3,8520 | 4,2208 |
| 14 | 0,6924 | 1,3450 | 1,7613 | 2,1448 | 2,6245 | 2,9768 | 3,3257 | 3,7874 | 4,1405 |
| 15 | 0,6912 | 1,3406 | 1,7530 | 2,1314 | 2,6025 | 2,9467 | 3,2860 | 3,7328 | 4,0728 |
| 16 | 0,6901 | 1,3368 | 1,7459 | 2,1199 | 2,5835 | 2,9208 | 3,2520 | 3,6862 | 4,0150 |
| 17 | 0,6892 | 1,3334 | 1,7396 | 2,1098 | 2,5669 | 2,8982 | 3,2224 | 3,6458 | 3,9651 |
| 18 | 0,6884 | 1,3304 | 1,7341 | 2,1009 | 2,5524 | 2,8784 | 3,1966 | 3,6105 | 3,9216 |
| 19 | 0,6876 | 1,3277 | 1,7291 | 2,0930 | 2,5395 | 2,8609 | 3,1737 | 3,5794 | 3,8834 |
| 20 | 0,6870 | 1,3253 | 1,7247 | 2,0860 | 2,5280 | 2,8453 | 3,1534 | 3,5518 | 3,8495 |
| 21 | 0,6864 | 1,3232 | 1,7207 | 2,0796 | 2,5176 | 2,8314 | 3,1352 | 3,5272 | 3,8193 |
| 22 | 0,6858 | 1,3212 | 1,7171 | 2,0739 | 2,5083 | 2,8188 | 3,1188 | 3,5050 | 3,7921 |
| 23 | 0,6853 | 1,3195 | 1,7139 | 2,0687 | 2,4999 | 2,8073 | 3.1040 | 3,4850 | 3,7676 |
| 24 | 0,6848 | 1,3178 | 1,7109 | 2,0639 | 2,4922 | 2,7969 | 3,0905 | 3,4668 | 3,7455 |
| 25 | 0,6844 | 1,3163 | 1,7081 | 2,0595 | 2,4851 | 2,7874 | 2,0782 | 3,4502 | 3,7251 |
| 26 | 0,6840 | 1,3150 | 1,7056 | 2,0555 | 2,4786 | 2,7787 | 3,0669 | 3,4350 | 3,7066 |
| 27 | 0,6837 | 1,3137 | 1,7033 | 2,0518 | 2,4727 | 2,7707 | 3,0565 | 3,4210 | 3,6896 |
| 28 | 0,6834 | 1,3125 | 1,7011 | 2,0484 | 2,4671 | 2,7633 | 3,0469 | 3,4082 | 3,6739 |
| 29 | 0,6830 | 1,3114 | 1,6991 | 2,0452 | 2,4620 | 2,7564 | 3,0380 | 3,3962 | 3,6594 |
| 30 | 0,6828 | 1,3104 | 1,6973 | 2,0423 | 2,4573 | 2,7500 | 3,0298 | 3,3852 | 3,6460 |
| 32 | 0,6822 | 1,3086 | 1,6939 | 2,0369 | 2,4487 | 2,7385 | 3,0149 | 3,3653 | 3,6218 |
| 34 | 0,6818 | 1,3070 | 1,6909 | 2,0322 | 2,4411 | 2,7284 | 3,0020 | 3,3479 | 3,6007 |
| 36 | 0,6814 | 1,3055 | 1,6883 | 2,0281 | 2,4345 | 2,7195 | 2,9905 | 3,3326 | 2,5821 |
| 38 | 0,6810 | 1,3042 | 1,6860 | 2,0244 | 2,4286 | 2,7116 | 2,9803 | 3,3190 | 3,5657 |
| 40 | 0,6807 | 1,3031 | 1,6839 | 2,0211 | 2,4233 | 2,7045 | 2,9712 | 3,3069 | 3,5510 |
| 42 | 0,6804 | 1,3020 | 1,6820 | 2,0181 | 2,4185 | 2,6981 | 2,9630 | 3,2960 | 3,5377 |
| 44 | 0,6801 | 1,3011 | 1,6802 | 2,0154 | 2,4141 | 2,6923 | 2,9555 | 3,2861 | 3,5258 |
| 46 | 0,6799 | 1,3002 | 1,6787 | 2,0129 | 2,4102 | 2,6870 | 2,9488 | 3,2771 | 3,5150 |
| 48 | 0,6796 | 1,2994 | 1,6772 | 2,0106 | 2,4066 | 2,6822 | 2,9426 | 3,2689 | 3,5051 |
| 50 | 0,6794 | 1,2987 | 1,6759 | 2,0086 | 2,4033 | 2,6778 | 2,9370 | 3,2614 | 3,4960 |
| 55 | 0,6790 | 1,2971 | 1,6730 | 2,0040 | 2,3961 | 2,6682 | 2,9247 | 3,2561 | 3,4764 |
| 60 | 0,6786 | 1,2958 | 1,6706 | 2,0003 | 2,3901 | 2,6693 | 2,9146 | 3,2317 | 3,4602 |
| 65 | 0,6783 | 1,2947 | 1,6686 | 1,9971 | 2,3851 | 2,6536 | 2,9060 | 3,2204 | 3,4466 |
| 70 | 0,6780 | 1,2938 | 1,6669 | 1,9944 | 2,3808 | 2,6479 | 2,8987 | 3,2108 | 3,4350 |
| 80 | 0,6776 | 1,2922 | 1,6641 | 1,9901 | 2,3739 | 2,6387 | 2,8870 | 2,1953 | 3,4163 |
| 90 | 0,6772 | 1,2910 | 1,6620 | 1,9867 | 2,3685 | 2,6316 | 2,8779 | 3,1833 | 3,4019 |
| 100 | 0,6770 | 1,2901 | 1,6602 | 1,9840 | 2,3642 | 2,6259 | 2,8707 | 3,1737 | 3,3905 |
| 120 | 0,6765 | 1,2886 | 1,6577 | 1,9799 | 2,3578 | 2,6174 | 2,8599 | 3,1595 | 3,3735 |
| 150 | 0,6761 | 1,2872 | 1,6551 | 1,9759 | 2,3515 | 2,6090 | 2,8492 | 3,1455 | 3,3566 |
| 200 | 0,6757 | 1,2858 | 1,6525 | 1,9719 | 2,3451 | 2,6006 | 2,8385 | 3,1315 | 3,3398 |
| 250 | 0,6755 | 1,2849 | 1,6510 | 1,9695 | 2,3414 | 2,5956 | 2,8322 | 3,1232 | 3,3299 |
| 300 | 0,6753 | 1,2844 | 1,6499 | 1,9679 | 2,3388 | 2,5923 | 2,8279 | 3,1176 | 3,3233 |
| 400 | 0,6751 | 1,2837 | 1,6487 | 1,9659 | 2,3357 | 2,5882 | 2,8227 | 3,1107 | 2,3150 |
| 500 | 0,6750 | 1,2832 | 1,6479 | 1,9647 | 2,3338 | 2,5857 | 2,8195 | 3,1066 | 3,3101 |
| ∞ | 0,6745 | 1,2816 | 1,6449 | 1,9600 | 2,3263 | 2,5758 | 2,8070 | 3, 0902 | 3,2905 |

