Rozkład chi2  – teoria

Teoria

Rozkład chi2 (chi kwadrat) to rozkład zmiennej losowej który powstał w wyniku przekształcenia rozkładu normalnego:
Niech Xi∼N(0,1) dla i = 1, 2, … k będą zmiennymi niezależnymi wtedy zmienna rozkładu chi kwadrat o k stopniach swobody χ2k wyraża się wzorem:

    \[\chi^{2}_{k} = \sum\limits_{i=1}^n X^{2}_{i}\]

Wykres rozkładu chi2 wygląda następująco:

rozkład chi-kwadrat (chi2)

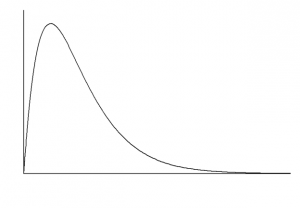
Cechy rozkładu:

Jak widać na rysunku wyżej, rozkład chi-kwadrat jest nieujemny o prawostronnej asymetrii(dłuższy prawy “ogon” rozkładu). Wraz ze wzrostem k wykres jest coraz bardziej spłaszczony i dłuższy – “ogon rozkładu wolniej opada”.

Rozkład chi-kwadrat służy do analizy wariancji(testowanie hipotez dla wariancji, wyznaczanie poziomów ufności, wyliczanie prawdopodobieństwa, że wariancja spełnia dany warunek), testów zgodności oraz testów niezależności.

Tablice

p- poziom prawdopodobieństwa

df- liczba stopni swobody

df \ p0,990,950,900,800,500,300,200,100,050,020,01
10,0000,0040,0160,0640,4551,0741,6422,7063,8415,4126,635
20,0200,1030,2110,4461,3862,4083,2194,6055,9917,8249,210
30,1150,3520,5841,0052,3663,6654,6426,2517,8159,83711,34
40,2970,7111,0641,6493,3574,8785,9897,7799,48811,6713,28
50,5541,1451,6102,3434,3516,0647,2899,23611,0713,3915,09
60,8721,6352,2043,0705,3487,2318,55810,6412,5915,0316,81
71,2392,1672,8333,8226,3468,3839,80312,0214,0716,6218,47
81,6462,7333,4904,5947,3449,52411,0313,3615,5118,1720,09
92,0883,3254,1685,3808,34310,6612,2414,6816,9219,6821,67
102,5583,9404,8656,1799,34211,7813,4415,9918,3121,1623,21
113,0534,5755,5786,98910,3412,9014,6317,2719,6722,6224,72
123,5715,2266,3047,80711,3414,0115,8118,5521,0324,0526,22
134,1075,8927,0428,63412,3415,1216,9819,8122,3625,4727,69
144,6606,5717,7909,46713,3416,2218,1521,0623,6826,8729,14
155,2297,2618,54710,3114,3417,3219,3122,3125,0028,2630,58
165,8127,9629,31211,1515,3418,4220,4623,5426,3029,6332,00
176,4088,67210,0812,0016,3419,5121,6124,7727,5930,9933,41
187,0159,39010,8612,8617,3420,6022,7625,9928,8732,3534,80
197,63310,1211,6513,7218,3421,6923,9027,2030,1433,6936,19
208,26010,8512,4414,5819,3422,7725,0428,4131,4135,0237,57
218,89711,5913,2415,4420,3423,8626,1729,6132,6736,3438,93
229,54212,3414,0416,3121,3424,9427,3030,8133,9237,6640,29
2310,2013,0914,8517,1922,3426,0228,3432,0135,1738,9741,64
2410,8613,8515,6618,0623,3427,1029,5532,2036,4140,2742,98
2511,5214,6116,4718,9424,3428,1730,6734,3837,6541,5744,31
2612,2015,3817,2919,8225,3429,2531,7935,5638,8842,8645,64
2712,8816,1518,1120,7026,3430,3232,9136,7140,1144,1446,96
2813,5616,9318,9421,5927,3431,3934,0337,9241,3445,4248,28
2914,2617,7119,7722,4728,3432,4635,1439,0942,5646,6949,59
3014,9518,4920,6023,3629,3433,5336,2540,2643,7747,9650,89

Wideo

Test Chi-kwadrat