Klasyczne miary rozkładu – teoria

Klasyczne miary rozkładu to takie, które uwzględniają wszystkie wartości uzyskane w próbie losowej. W związku z tym, zmiana dowolnego elementu próby powoduje zmianę wartości miary.
Do miar klasycznych zaliczamy:

  • średnią arytmetyczną
  • wariancję
  • współczynnik skośności
  • momenty centralne
  • momenty zwykłe

Średnia arytmetyczna

Teoria

Średnia jest najprostszą miarą stosowaną w analizie danych. Często jest kojarzona jako wartość leżąca blisko środka danej zbiorowości. Informuje nas o tym jakiej wartości możemy się spodziewać przy analizie losowej obserwacji. Jednakże średnia nie zawsze zwraca wartość możliwą w rzeczywistości.

Np. Co oznacza sformułowanie, że średnia liczba samochodów posiadanych przez rodzinę jest równa 1.23 ?

Możemy zinterpretować to stwierdzenie w ten sposób, że przeciętna rodzina ma ok. 1 samochodu, ale pewna część rodzin posiada co najmniej 2 auta(prawdopodobnie istnieją także rodziny posiadające 0, zaniżające średnią).
Musimy jednak pamiętać, że istnieje również możliwość, że żadna z rodzin nie posiada 1 samochodu, a istnieją wyłącznie rodziny z 0 lub kilkoma samochodami. Dzieje się tak, ponieważ średnie są silnie narażone na działanie wartości skrajnych.

Wzory

Rodzaje szeregów:

a) SZCZEGÓŁOWY 

    \[\overline{X} = \frac{1}{n} \sum\limits_{i=1}^n X_{i}\]

b) ROZDZIELCZY-ILOŚCIOWY 

    \[\overline{X} = \frac{1}{n} \sum X_{i} \cdot n_{i}\]

c) ROZDZIELCZY-CZESTOŚCIOWY 

    \[\overline{X}= \sum X_{i} \cdot \omega_{i}\]

d) PRZEDZIAŁOWY – ILOŚCIOWY 

    \[\overline{X} = \frac{1}{n} \sum \overline{X}_{i} \cdot n_{i}\]

e) PRZEDZIAŁOWY – CZĘSTOŚCIOWY 

    \[\overline{X}= \sum \overline{X}_{i} \cdot \omega_{i}\]

Oznaczenia:

n – ilość obserwacji

Xi – wartość i-tej obserwacji

wi – częstość i-tej obserwacji lub przedziału

    \[\overline{X}_{i}\]

– wartość środkowa i-tego przedziału

Wideo

Średnia arytmetyczna

Wariancja

Teoria

Wariancja jest najczęściej wykorzystywaną w statystyce miarą zróżnicowania danej cechy. Pozwala nam ona określić o ile obserwacje odbiegają o średniej. Dana cecha może być silnie zróżnicowana(duża liczba obserwacji oddalonych od średniej) lub słabo zróżnicowana(większość obserwacji leży blisko średniej)
Wariancja jest momentem centralnym drugiego rzędu zmiennej losowej. Najczęściej obliczana ze wzoru:

    \[D^{2}(X)=E(X^{2})-[E(X)]^{2}\]

Odchylenie standardowe to pierwiastek z wariancji.

    \[\sigma = \sqrt{VarX}\]

Wzory

Rodzaje szeregów:

SZCZEGÓŁOWY: 

    \[VarX = \frac{1}{n} \sum\limits_{i=1}^n (X_{i}- \overline{X})^{2}\]

ROZDZIELCZY-ILOŚĆIOWY: 

    \[VarX = \frac{1}{n} \sum (X_{i}- \overline{X})^{2}\cdot n_{i}\]

ROZDZIELCZY-CZĘSTOŚCIOWY: 

    \[VarX= \sum(X_{i}- \overline{X})^{2} \cdot \omega_{i}\]

PRZEDZIAŁOWY-ILOŚCIOWY: 

    \[VarX = \frac{1}{n} \sum (X_{i}- \overline{X})^{2} \cdot n_{i}\]

PRZEDZIAŁOWY-CZĘSTOŚCIOWY: 

    \[VarX = \sum (X_{i}- \overline{X})^{2} \cdot \omega_{i}\]

Legenda:

n – ilość obserwacji

Xi – wartość i-tej obserwacji

ni – liczebność i-tej obserwacji/przedziału

ωi – częstość i-tej obserwacji/przedziału

wartość środkowa i-tego przedziału: 

    \[\overline{X}_{i}\]

Współczynnik asymetrii(skośności)

Teoria

Współczynnik asymetrii(skośności) pozwala określić w jaki sposób rozłożone są dane, tzn. czy dane są symetrycznie(równomiernie) rozłożone po obu stronach średniej, czy któraś strona jest dominująca – np. więcej obserwacji leży po prawej stronie, położone są dalej od średniej.

Współczynnik skośności określony jest wzorem: 

    \[A_{s} = \frac{ \overline{X} - D }{s}\]

Wynik interpretuje się w taki sposób:

  1. Jeżeli As>0 to występuje asymetria prawostronna, czyli prawa strona jest “dłuższa”
  2. Jeżeli As<0 to występuje asymetria lewostronna, czyli lewa strona jest “dłuższa”
  3. Jeżeli As=0 to asymetria nie występuje.

Graficzna prezentacja

asymetria lewostronna

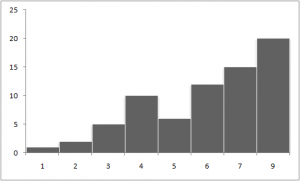
1)As<0 – asymetria lewostronna

asymetria prawostronna

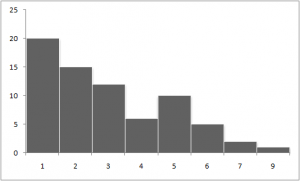
2) As>0 – asymetria prawostronna

rozkład symetryczny

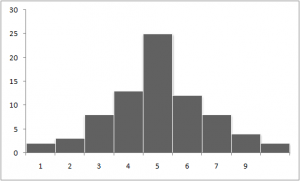
3) As=0 – brak asymetrii(rozkład symetryczny)

Momenty centralne

Teoria

Wyróżniamy 4 momenty centralne. Każdy z nich tak na prawdę odpowiada jednej z miar wykorzystywanych w statystyce. Momentem centralnym nazywamy średnią arytmetyczną odchyleń poszczególnych wartości zmiennej od średniej, podniesionych do potęgi r.

Moment centralny pierwszego rzędu zawsze jest równy 0

Momentem centralnym drugiego rzędu nazywamy wariancję.

Momentem centralnym trzeciego rzędu nazywamy współczynnik asymetrii(skośności)

Momentem centralnym czwartego rzędu nazywamy współczynnik kurtozy(miara koncentracji obserwacji)

Wzory

    \[m_{r}=\frac{1}{n}\sum_{i=1}^{k}(x_{i}-\overline{x})^{r}\]

Legenda:

r – rząd, stopień momentu

mr – moment centralny r-tego stopnia

xi – poszczególne obserwacje

n – liczba obserwacji

    \[\overline{x} - srednia\]

Klasyczne miary rozkladu - napis